Azon nem tudunk változtatni, hogy emberek vagyunk és hogyan van behuzalozva az agyunk. Szinte az összes tapasztalatunk a LINEÁRIS gondolkodás felé mutat. Ha most fektetek be energiát, akkor most akarok jutalmat. Ha most vadászok, akkor most szeretném a gazella húsát. Ebben az órában is egy óra telt el és a következőben is egy óra fog eltelni. Ha kétszer olyan erős vagyok, kétszer akkora súlyt tudok felemelni. Ha elindulok autóval Szegedre adott sebességgel, akkor X időbe fog telni. Világos.
Az exponenciális gondolkodásra példa egy baktérium osztódása. Az első fél órában az 1 baciból 2 lesz. Aztán a 2-ből 4, majd 8, 16, 32, stb. Tehát ahogy telik az idő, nem egységnyi változás történik, hanem a folyamat gyorsul vagy éppen lassul. Ezt nevezzük EXPONENCIÁLIS változásnak. Nézzünk meg erre egy kevésbé ismert példát, eztán megnézzük miért jó neked, ha ez is a fejedben van.
Javaslom nézd meg inkább videós formában:
Ha nem szeretnél lemaradni a hasznos újdonságokról, akkor klikkelj ide és iratkozz fel a Youtube csatornámra!
I
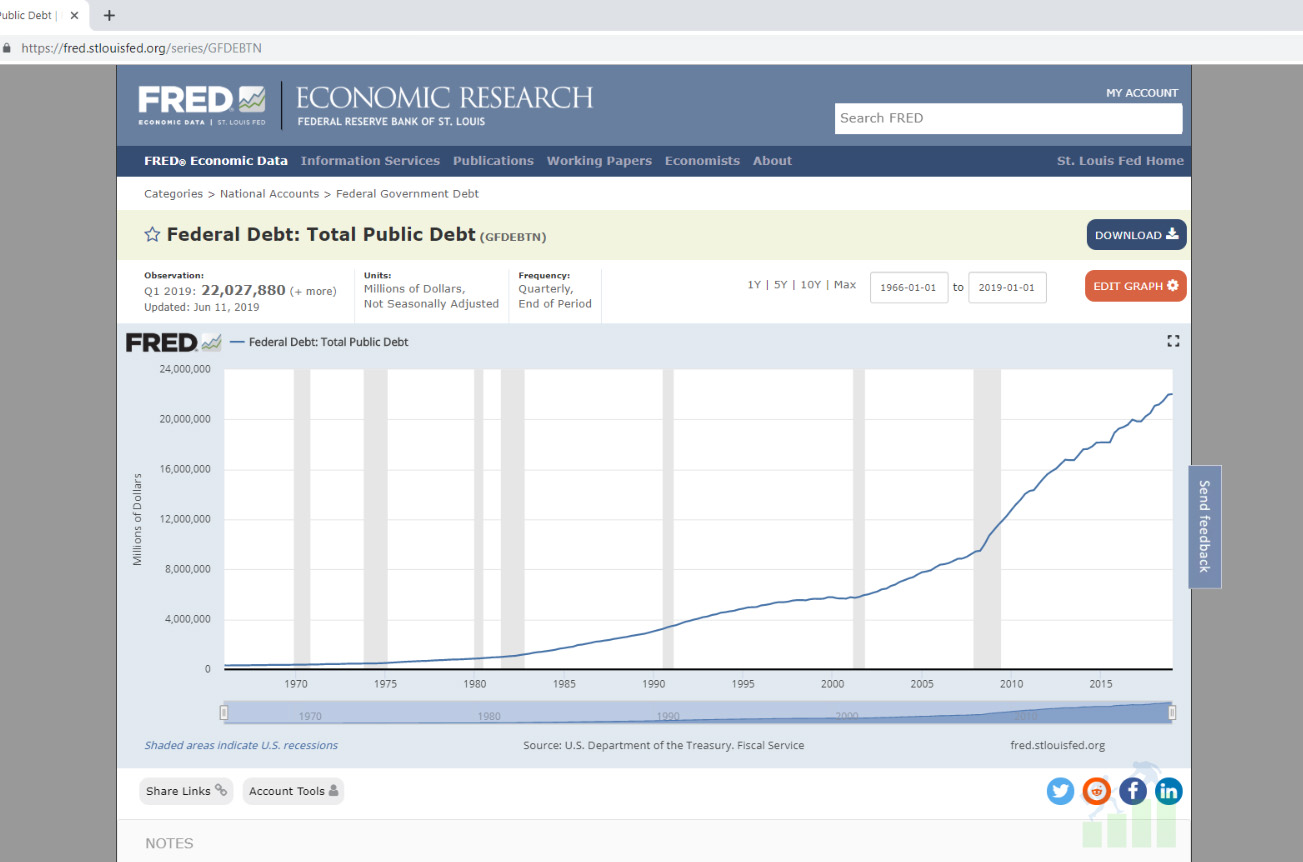
Te is felmehetsz a FRED honlapjára és letöltheted az amerikai államadósság adatait mondjuk 1966-tól napjainkig.
I
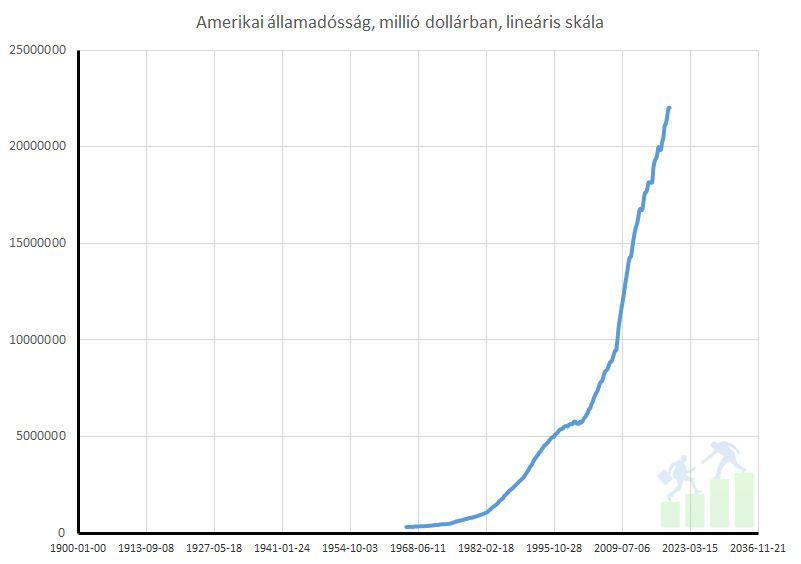
Ezt letöltöttem Excelben és az alábbi kép fogadott. Ez bizony egy hiperbola jobb oldala, vagy hokiütő forma görbe, nem kell sokat magyarázni, elszáll mint a rakéta, feltört mint a cipő sarka.
I
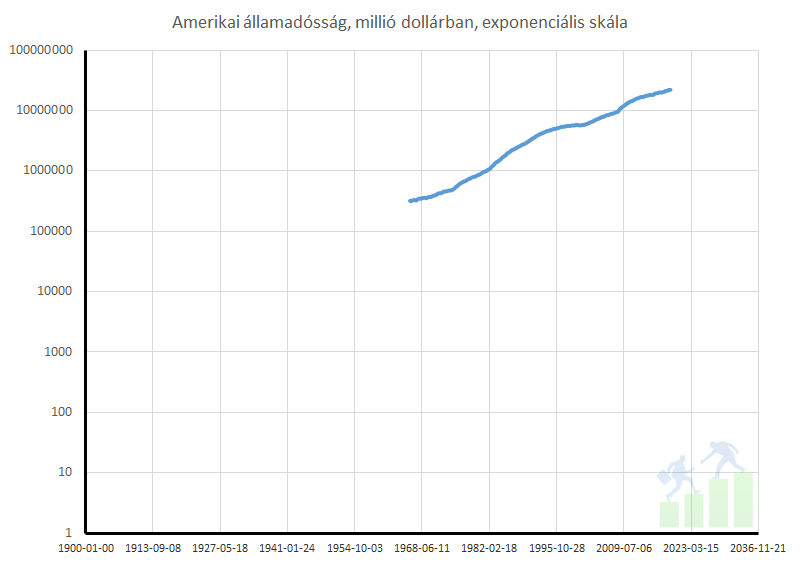
De érdemes megnézned, hogy az ábra bal oldali skála lineáris. Minden egységnyi lépés 5 trillió dollárnak felel meg. Ettől lineáris a skála. Most nézzük meg ugyanezt az ábrát, ha a bal oldali skálát átállítom logaritmikussá. Tehát a következő ábrán már minden egység tízszeres változást jelent!
I
Az a hiperbola átalakult egy egyenes vonallá (kis túlzással). Ha valami exponenciális (most éppen logaritmikus) skálán egyenes vonalt ad, akkor az exponenciálisan változik. És valóban, az amerikai államadósság 8-10 évente megduplázódik. Ezért mondja Ron Paul már évtizedek óta, hogy gond van, mert ő tud exponenciálisan gondolkodni. A problémát már abban a pillanatban lehet látni, hogy a baktérium elkezd osztódni, de a legtöbb ember csak akkor veszi észre, amikor már majdnem ellepik a medencét a bacik.
És mivel nagyon nehezen tudunk exponenciálisan gondolkodni, ezért nehéz elfogadni a kamatos kamat elvét. Talán mindenki megérti, de nincs igazán a vérünkben, hogy ennek időt kell adni, mire igazán kifejti a hatását. Ezért nem adunk neki időt.
Így van ez a kamatos költséggel is. Hiszen az is „kamatozik”. Minél hosszabb időtávon nézzük, annál fájóbb mennyi pénzt vesznek el tőlünk a kis költségek által. Az 1-2 %-os költség nem tűnik nagynak, pedig az már borzasztó nagy hosszú időre vetítve. És ezért sem könnyű belátni, hogy adott termékek mellé az állam valóban ad adótámogatást, de a költségek hosszú távon nézve már elviszik az egészet.
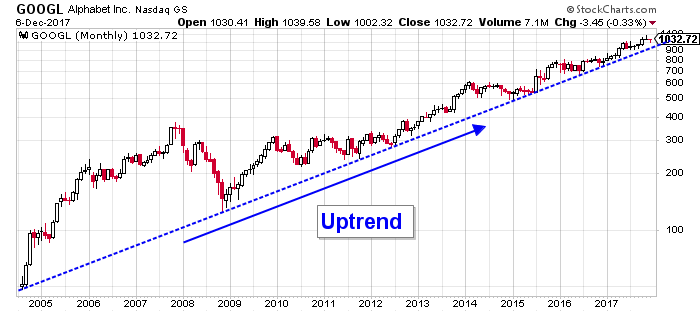
Ezért éri meg exponenciálisan gondolkodni, a világban sok folyamat exponenciálisan működik, csak nem vagyunk rá tréningezve, hogy tudatosuljon bennünk. Ilyen még amikor az osztalékodat visszaforgatod, ahogy a fa növekszik és több levelet képez egyre gyorsabban tud növekedni vagy ahogyan egy kis tech vállalat növekedésnek indul. A részvények árfolyamát is nézheted logaritmikus skálán, ez itt alább csak egy példa.
I
De ilyen az infláció hatása is, igen ez a reklám helye, aki olvasta a második könyvem, annak nem meglepetés mit okozott az infláció az embereknek az elmúlt évtizedekben. De ezért szeretnénk gyorsan meggazdagodni is, hiszen ha most vállalunk nagy kockázatot, akkor most is szeretnénk a jutalmat és ezt sok rossz szándékú ember kihasználja.
És van még egy példa, de azt már egy külön epizódban fogom bemutatni.
Ha tudsz még remek példákat, élethelyzeteket, akkor oszd meg velünk!
I
Nos, azt hiszem már elég hosszúra sikeredett ez a cikk, de remélem hasznos volt számodra! Ha így van, kérlek támogasd a munkámat annyival, hogy megosztod másokkal is, követed a Facebook oldalam, feliratkozol a Youtube csatornámra vagy a hírlevelemre itt.
Katt ide és nézd meg ezt a cikket videós formában is!Kérdezz bármit a Telegram app-on keresztül!Csatlakozz a Facebook oldalhoz, hogy ne maradj le semmirol!




Trackback/Pingback