A számok csak nem hazudnak! Egyik olvasóm, Sándor, nem érti mi folyik a politikában. Hogyan lehet az, hogy ugyanarról a dologról beszélünk, ugyanazokat a számokat nézzük, mégis két teljesen ellentétes eredményre jutunk? Mondjam már el a véleményem, mert ő már nem tudja kinek hihet. Én megpróbálok kimaradni a politikából, de mégis választ adok a két példára.
Szeretnéd inkább megnézni ezt videós formában? Tessék:
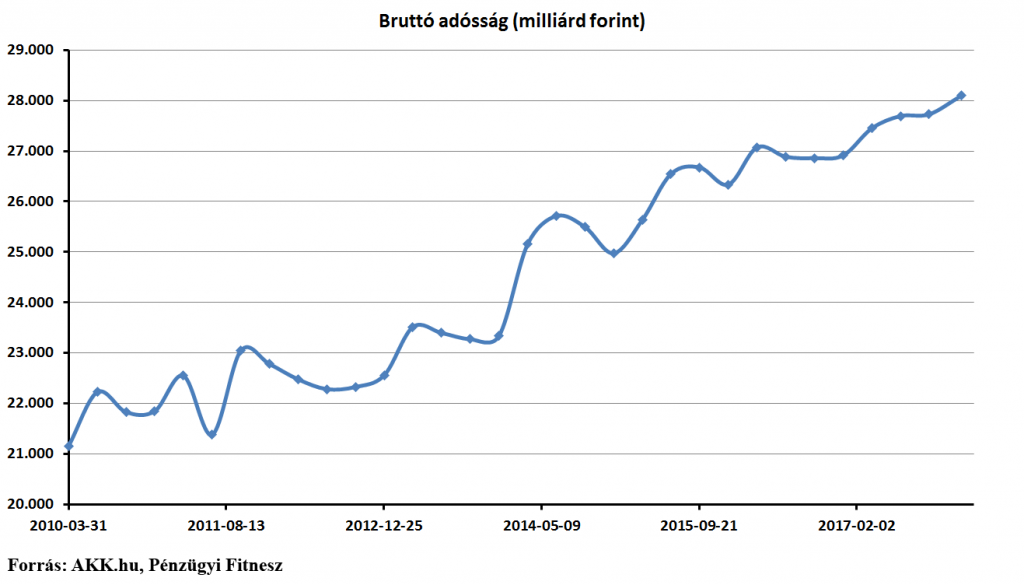
Államadósság
Az első példa az államadósság. Az egyik fél szerint csökken az államadósság, a másik fél szerint növekszik. Hogy melyik félnek van igaza, a képek után kiderül.
Szerintem mindkét félnek igaza van, ahogy a fenti ábrákból kiderül. (Az adatokat az akk.hu weboldal jobb felső sarkában található „Adósság” kockából vettem. Onnan letölthető az adatsor.) Egyszerűen csak arról van szó, hogy almát hasonlítunk körtéhez. GDP arányosan valóban csökken az adósság, de attól még a nominális összeg, hogy ez hány ezer milliárd forint, az növekszik. Senki nem hazudik, csak más számokat néznek. Mondjuk azért, mert egyikük szerint a GDP arányos számsort nézi mindenki, tehát azt kell követni, a másik szerint pedig visszafizetni a nominális összeget kell, tehát az a fontos. Más számokat nézni áll érdekükben, de mégis mindkettőnek igaza van és mindkét fél szerint a másik hazudik!
Utolérjük Ausztriát
A másik ilyen olvasói probléma a GDP növekedéssel volt. Az egyik fél azt mondja, hogy a mi 4%-os növekedésünk az nagyobb, mint Ausztria 2%-os növekedése (pontosan nem emlékszem, de körülbelül ezek a számok). Ezért aztán egyre inkább utolérjük Ausztriát. A másik oldalról viszont azt hallod, hogy Ausztria GDP-je jobban növekszik. Kinek van igaza?
Ismét oda lyukadunk, ki, hogy mindegyik félnek igaza van. Egyrészt a 4%-os növekedés az több, mint a 2%, ez világos, tehát igaza van. Másrészt pedig Ausztriának durván háromszor akkora a GDP-je és ha egy háromszor akkora szám növekedik fele olyan mértékben, az végül is magasabb növekedés:
Magyarország: 123.494 milliárd euro + 4% = 128.434 milliárd euro –> növekedés: 4.94 milliárd euro
Ausztria: 369.685 milliárd euro + 2% = 377.079 milliárd euro –> növekedés: 7.39 milliárd euro
Mi ebből a tanulság? A tudományban ez gyakran előfordul.
Három fő dolog jut eszembe ezzel kapcsolatban.
1. Egyrészt azt ajánlom, hogy legyél mindig kicsit kritikus a számokkal szemben. Az én tudományos hátteremmel azt tudom mondani, hogy nagyon sokat számít hogyan prezentálod a számokat. Melyik részét mutatod meg az oszlopdiagramnak? Más formát mutathat a számsor ha például logaritmikus skálát használsz és ez képes befolyásolni az emberi agyat. Ugyanabba a számsorba más emberek képesek más eredményt belelátni! Sok ilyet kell látni, sok grafikont kell értelmezni, hogy kialakuljon az emberben ez az érzék. Nem Sándor az első, aki felveti ezt a problémát. Ezen szinte minden Ph.D. hallgató át kell verekedje magát és van egy zseniális könyv is a témában, Darrell Huff: How to lie with statistics. Nagyon jól illusztrálja hogyan lehet elfedni a valóságot a statisztikával.
2. Ezt nem tanítják az iskolában, de mint választópolgároknak, nekünk kell eldönteni melyik logika ésszerűbb. A mi dolgunk, hogy objektíven szemléljük ezeket és az is, hogy eldöntsük melyik megoldás fontosabb számunka. Nem az, hogy melyik fél hazudik! A fenti példákban jogilag nem hazudnak, mégis eldönthetjük, hogy az alma vagy a körte fontosabb számunkra, melyik áll közelebb a saját értékrendünkhöz, melyik magyarázatnak van több értelme. Először döntsük el, hogy egy témával kapcsolatban milyen logika mentén érdemes haladni, mi a kérdés valójában és csak utána keressük meg aki arról beszél.
3. Harmadrészt, én ugye klinikai vizsgálatokkal foglalkozom. Ha ugyanazt a vérmintát megmérjük a laborban két különböző analitikai módszerrel, akkor két különböző eredményt fogunk kapni. Ez nem jelenti azt, hogy az egyik hazudik, csak éppen más kérdésre ad választ, más elven működik. Például az ELISA módszer csak a biológiailag aktív fehérjéket mutatja ki, míg a tömegspektrométer az összes fehérjét. Először el kellene dönteni, hogy mire vagyunk kíváncsiak és csak utána lenne szabad módszert választani.
Béla, az átlag választópolgár pedig fordítva ül a lovon, először választ módszert (pártot) és utána jönnek a számok, lenyeli azokat, bármit is mutassanak. Nyilván a másik módszer (párt) eredménye ütközik ezzel, tehát szerinte az hazugság lesz. Elhiszi amit mér, de nem érti, hogy az mire ad választ. Pedig először el kellene döntenie mit érdemes vizsgálni és aztán ehhez módszert keresni.
El kellene (tudni) dönteni, hogy például az államadósság méreténél mi a fontosabb? Mivel lennénk elégedettek? Szívünk joga úgy dönteni, hogy a GDP-hez viszonyítjuk. Akkor ehhez keresünk módszert és arra hallgatunk aki erről beszél. Ha viszont fontosabb annak a valódi mérete, akkor olyan emberre figyeljünk aki meg arról beszél. Abban megegyezhetünk, hogy végül szeretnénk mindkét mutatót nullában látni.
Ezek csak példák voltak és nem teszem le a voksomat egyik megoldás mellett sem. De nagyon fontos azt látni, hogy bár a számok nem hazudnak, mégis attól függően, hogy mi a kérdésünk, a számokba bele lehet látni két ellentétes véleményt és a mi feladatunk megnézni, hogy ezek mögött mi a logika és eldönteni számunkra melyik logika fontosabb. Ja, és próbáljunk nyitottak lenni mások véleményére is legalább néha, hiszen mi is hibázhatunk és együtt sokkal nagyobb szürke állományunk van…
Segített ez a cikk valamit Bélának? Neked segített? Ha igen, kérlek oszd meg másokkal is! Ha nekem szeretnél segíteni, iratkozz fel a hírlevelemre (ritkán kapsz tőlem levelet, akkor is a te érdekedben) és ha nem szeretnél semmiről sem lemaradni, akkor kövesd a Facebook oldalam! Annak is örülnék, ha megosztanád a véleményed alul!
Katt ide és nézd meg ezt a cikket videós formában is!Kérdezz bármit a Telegram app-on keresztül!Csatlakozz a Facebook oldalhoz, hogy ne maradj le semmirol!





Trackback/Pingback